堆排序
堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。
堆是一个近似完全二叉树的结构，并同时满足堆的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。
基础知识 JCIP-11-二叉堆
最大堆
若以升序排序说明，把数组转换成最大堆(Max-Heap Heap)，这是一种满足最大堆性质(Max-Heap Property)的二叉树：对于除了根之外的每个节点i, A[parent(i)] ≥ A[i]。
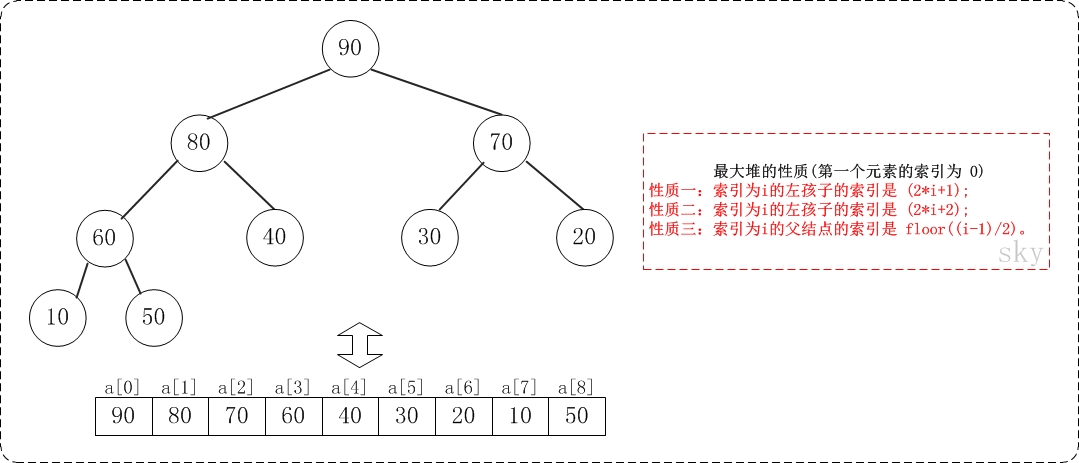
堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：
重复从最大堆取出数值最大的结点(把根结点和最后一个结点交换，把交换后的最后一个结点移出堆)，并让残余的堆维持最大堆性质。
同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子:
堆节点的访问
通常堆是通过一维数组来实现的。
在数组起始位置为0的情形中：
则父节点和子节点的位置关系如下：
(01) 索引为i的左孩子的索引是 (2*i+1);
(02) 索引为i的左孩子的索引是 (2*i+2);
(03) 索引为i的父结点的索引是 floor((i-1)/2);
堆的操作
在堆的数据结构中，堆中的最大值总是位于根节点（在优先队列中使用堆的话堆中的最小值位于根节点）。
堆中定义以下几种操作：
最大堆调整（Max Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
创建最大堆（Build Max Heap）：将堆中的所有数据重新排序
堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算
堆排序算法图解
这个图解来自 图解排序算法(三)之堆排序，画的非常漂亮。
基本思想
将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。
将其与末尾元素进行交换，此时末尾就为最大值。
然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。
步骤
步骤一 构造初始堆
将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。
a. 假设给定无序序列结构如下
b. 此时我们从最后一个非叶子结点开始（叶子结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。
c. 找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。
d. 这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。
此时，我们就将一个无序的序列构造成了一个大顶堆。
步骤二 调整堆
将堆顶元素与末尾元素进行交换，使末尾元素最大。
然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。
a. 将堆顶元素9和末尾元素4进行交换
b. 重新调整结构，使其继续满足堆定义
c. 再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.
后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序
简单总结
再简单总结下堆排序的基本思路：
a. 将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
b. 将堆顶元素与末尾元素交换，将最大元素”沉”到数组末端;
c. 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。
java 实现
说明
为了和前面的逻辑保持一致，我们暂时依然使用 list 去实现这个堆排序。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77package com.github.houbb.sort.core.api;
import com.github.houbb.log.integration.core.Log;
import com.github.houbb.log.integration.core.LogFactory;
import com.github.houbb.sort.core.util.InnerSortUtil;
import java.util.List;
/**
* 堆排序
*
* @author binbin.hou
* @since 0.0.4
*/
public class HeapSort extends AbstractSort {
private static final Log log = LogFactory.getLog(HeapSort.class);
@Override
@SuppressWarnings("all")
protected void doSort(List<?> original) {
final int maxIndex = original.size() - 1;
/*
* 第一步：将数组堆化
* beginIndex = 第一个非叶子节点。
* 从第一个非叶子节点开始即可。无需从最后一个叶子节点开始。
* 叶子节点可以看作已符合堆要求的节点，根节点就是它自己且自己以下值为最大。
*/
int beginIndex = original.size() / 2 - 1;
for (int i = beginIndex; i >= 0; i--) {
maxHeapify(original, i, maxIndex);
}
/*
* 第二步：对堆化数据排序
* 每次都是移出最顶层的根节点A[0]，与最尾部节点位置调换，同时遍历长度 - 1。
* 然后从新整理被换到根节点的末尾元素，使其符合堆的特性。
* 直至未排序的堆长度为 0。
*/
for (int i = maxIndex; i > 0; i--) {
InnerSortUtil.swap(original, 0, i);
maxHeapify(original, 0, i - 1);
}
}
/**
* 调整索引为 index 处的数据，使其符合堆的特性。
*
* @param list 列表
* @param index 需要堆化处理的数据的索引
* @param len 未排序的堆（数组）的长度
* @since 0.0.4
*/
@SuppressWarnings("all")
private void maxHeapify(final List list, int index, int len) {
int li = (index * 2) + 1; // 左子节点索引
int ri = li + 1; // 右子节点索引
int cMax = li; // 子节点值最大索引，默认左子节点。
// 左子节点索引超出计算范围，直接返回。
if (li > len) {
return;
}
// 先判断左右子节点，哪个较大。
if (ri <= len && InnerSortUtil.gt(list, ri, li)) {
cMax = ri;
}
if (InnerSortUtil.gt(list, cMax, index)) {
InnerSortUtil.swap(list, cMax, index); // 如果父节点被子节点调换，
maxHeapify(list, cMax, len); // 则需要继续判断换下后的父节点是否符合堆的特性。
}
}
}
测试
1
2
3
4List<Integer> list = RandomUtil.randomList(10);
System.out.println("开始排序：" + list);
SortHelper.heap(list);
System.out.println("完成排序：" + list);
日志如下：
1
2开始排序：[48, 6, 85, 16, 93, 13, 0, 68, 68, 18]
完成排序：[0, 6, 13, 16, 18, 48, 68, 68, 85, 93]
开源地址
为了便于大家学习，上面的排序已经开源，开源地址：
欢迎大家 fork/star，鼓励一下作者~~
小结
堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n)，在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)…1]逐步递减，近似为nlogn。
所以堆排序时间复杂度一般认为就是O(nlogn)级。
ps: 个人理解一般树的数据结构，时间复杂度都是 logn 级别的。
希望本文对你有帮助，如果有其他想法的话，也可以评论区和大家分享哦。
各位极客的点赞收藏转发，是老马持续写作的最大动力！
